Difference between revisions of "Morphological dictionary"
(→Determinism: wider image) |
Objectivesea (talk | contribs) (Mainly punctuation improvements; corrected apparent error in caption for ''Image:Finite-state transducer wound wounds.svg''; changed ''on the right'' to''above'' to prevent confusion) |
||
| Line 1: | Line 1: | ||
{{TOCD}} |
{{TOCD}} |
||
| − | This page intends to describe how and why the '''morphological dictionaries''' in Apertium work the way they do. Descriptions will be presented, along with examples in code. It is hoped that this will help people understand how the dictionaries work without needing to wade through pages of equations. Morphological dictionaries in Apertium (or more properly [[lttoolbox]]) are based on finite-state transducer technology |
+ | This page intends to describe how and why the '''morphological dictionaries''' in Apertium work the way they do. Descriptions will be presented, along with examples in code. It is hoped that this will help people understand how the dictionaries work without needing to wade through pages of equations. Morphological dictionaries in Apertium (or more properly [[lttoolbox]]) are based on finite-state transducer technology; in this way they can also be referred to as ''lexical transducers''. The task of a morphological dictionary is to model the rules that govern the internal structure of words in a language. |
For example, speakers of English realise that the words "dog" and "dogs" are related, that "dogs" is to "dog" as "cats" is to "cat". The rules understood by the speaker reflect specific patterns and regularities in the way in which words are formed from smaller units and how those smaller units interact. |
For example, speakers of English realise that the words "dog" and "dogs" are related, that "dogs" is to "dog" as "cats" is to "cat". The rules understood by the speaker reflect specific patterns and regularities in the way in which words are formed from smaller units and how those smaller units interact. |
||
| − | Finite-state transducers are not the only way to model these rules |
+ | Finite-state transducers are not the only way to model these rules. It is also possible to write the rules in scripting languages such as perl or python, or as a lexer (examples include the Buckwalter morphological analyser for Arabic, or IceMorphy for Icelandic). There are however a number of downsides to this method: |
| − | * The analysers created are not reversible |
+ | * The analysers created are not reversible; that is, you cannot use the same model to analyse ''and'' generate. |
| − | * As the rule content may be both imperative and declarative, programs can be more complicated to understand and edit |
+ | * As the rule content may be both imperative and declarative, programs can be more complicated for non-experts to understand and edit. |
| − | In contrast, finite-state transducers are |
+ | In contrast, finite-state transducers are both reversible (the same description can be used for both analysis and generation) and declarative (a ''description'' of the morphological rules is separate from the algorithm which processes them). Note that analysers may also be described as decorated tries or finite-state acceptors (for example [[hunmorph]]); this may be declarative but non-reversible (i.e. not applicable to generation). |
[[Image:Finite-state acceptor beer.svg|right|thumb|125px|A finite-state acceptor for the string "beer".]] |
[[Image:Finite-state acceptor beer.svg|right|thumb|125px|A finite-state acceptor for the string "beer".]] |
||
==Finite-state automata== |
==Finite-state automata== |
||
| − | To start with it is worth defining |
+ | To start with, it is worth defining a finite-state automaton and how the two main types differ. This will not be an exhaustive description, just an overview so that the difference can be distinguished for the purposes of this article. To begin with, some terminology; if you are familiar with graphs (as in the data structure), this might help. A finite-state automaton can be visualised as a graph, with the nodes representing '''states''' and the arcs representing '''transitions'''. |
===Acceptors=== |
===Acceptors=== |
||
| − | A finite-state acceptor (or '''recogniser'''), as seen to the right, is an automaton which accepts or rejects input strings. |
+ | A finite-state acceptor (or '''recogniser'''), as seen to the right, is an automaton which accepts or rejects input strings. Taking the example at the right, we can see the automaton has: |
* a number of possible '''input characters''', or '''alphabet''' (the characters 'b', 'e' and 'r'), denoted as <math>\Sigma</math> |
* a number of possible '''input characters''', or '''alphabet''' (the characters 'b', 'e' and 'r'), denoted as <math>\Sigma</math> |
||
| − | * a '''start state''' |
+ | * a '''start state'''; in formal definitions this is usually labelled <math>s_0</math> |
* a number of intermediate '''states''', often denoted by <math>S</math> |
* a number of intermediate '''states''', often denoted by <math>S</math> |
||
* two '''final states''', denoted by <math>F</math> |
* two '''final states''', denoted by <math>F</math> |
||
| Line 48: | Line 48: | ||
</source> |
</source> |
||
</div> |
</div> |
||
| − | When the input on <code>stdin</code> is "beer", output {{sc|yes}} |
+ | When the input on <code>stdin</code> is "beer", output {{sc|yes}}; otherwise output {{sc|no}}, |
[[Image:Finite-state acceptor be ast r.svg|thumb|125px|right|This finite-state acceptor will accept any string defined by the regular expression <code>be*r</code>, i.e. br, ber, beer, beeer, beeeer, ...]] |
[[Image:Finite-state acceptor be ast r.svg|thumb|125px|right|This finite-state acceptor will accept any string defined by the regular expression <code>be*r</code>, i.e. br, ber, beer, beeer, beeeer, ...]] |
||
<pre> |
<pre> |
||
| Line 57: | Line 57: | ||
No |
No |
||
</pre> |
</pre> |
||
| − | It is worth noting that a finite-state acceptor can accept any string that can be defined by a regular expression. For example, if we want to accept the expression <code>bee*r</code>, |
+ | It is worth noting that a finite-state acceptor can accept any string that can be defined by a regular expression. For example, if we want to accept the expression <code>bee*r</code>, which can also be written <code>be+r</code> — that is, "b" followed by one or more "e" followed by "r" (e.g. ber, beer, beeer, ...) — we could do it with a finite-state acceptor. Finite-state acceptors can be used in applications such as spell-checking, where one of the basic tasks is to check if a word exists or not in a list of words. Using an acceptor is more efficient than the equivalent list, for reasons which will be outlined below. |
| Line 63: | Line 63: | ||
===Transducers=== |
===Transducers=== |
||
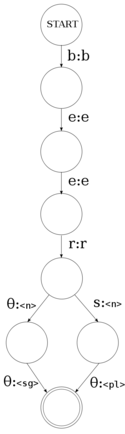
| − | [[Image:Finite-state transducer beer.svg|thumb|right|125px|A finite-state transducer for the strings "beer" and "beers" |
+ | [[Image:Finite-state transducer beer.svg|thumb|right|125px|A finite-state transducer for the strings "beer" and "beers"; the output is the ''lemma'' of the word, "beer", the ''part-of-speech'', <code><n></code> for "noun" and then the number, either singular (<code><sg></code>) or plural (<code><pl></code>).]] |
| − | Whilst acceptors are useful, for morphological analysis we need something that will give us an output for a given input. For example, given a [[surface form]] of a word, it will give us the [[lexical form]] (analysis) or given the lexical form it will give us the surface form (generation). For this, we need a '''transducer'''. A transducer is very much like an acceptor, with |
+ | Whilst acceptors are useful, for morphological analysis we need something that will give us an output for a given input. For example, given a [[surface form]] of a word, it will give us the [[lexical form]] (analysis); or given the lexical form, it will give us the surface form (generation). For this, we need a '''transducer'''. A transducer is very much like an acceptor, with this main difference: instead of each transition consuming a character from the input, each transition consumes a character and outputs a character. So instead of having a symbol on each arc, we have a tuple, input and output (see diagram to the right). |
| − | The diagram to the right shows a finite-state transducer<ref>In particular this is a "letter transducer" |
+ | The diagram to the right shows a finite-state transducer<ref>In particular this is a "letter transducer"; that is, each transition is modelled as an arc between two letters in the alphabet</ref> for the strings "beer" and "beers". This transducer has: |
* an '''input alphabet''', <math>\Sigma</math> (the characters 'b', 'e', 'r' and 's') |
* an '''input alphabet''', <math>\Sigma</math> (the characters 'b', 'e', 'r' and 's') |
||
| Line 107: | Line 107: | ||
====Determinism==== |
====Determinism==== |
||
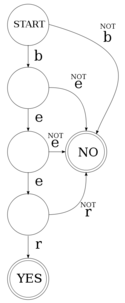
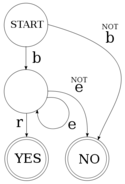
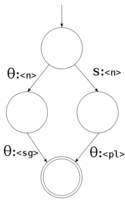
| − | [[Image:Finite-state transducer wound wounds.svg|thumb|200px|right|A non-deterministic finite-state transducer for three strings: wound, wounds. |
+ | [[Image:Finite-state transducer wound wounds.svg|thumb|200px|right|A non-deterministic finite-state transducer for three strings: wind, wound, wounds.]] |
| − | The transducer |
+ | The above transducer is '''deterministic'''; that is, for any given state and input symbol, it can only pass on to one state, or accept. In contrast, a '''non-deterministic''' transducer (as on the right) is one which from a given state and input symbol can branch to more than one state. That is, it can take more than one path through the transducer simultaneously. Note that although the transducer on the right branches, it branches in a deterministic way; after consuming the string "beer", it can either step to <code>(s:<n>)</code> if the next input symbol is 's', or <code>(θ:<n>)</code> otherwise. |
A non-deterministic finite-state transducer is modelled as: |
A non-deterministic finite-state transducer is modelled as: |
||
| Line 115: | Line 115: | ||
| − | The benefit of non-deterministic transducers over deterministic transducers is that they allow us to capture the ambiguity inherent in human language. For example the word "wound" in English can be a noun ("I have a wound") |
+ | The benefit of non-deterministic transducers over deterministic transducers is that they allow us to capture the ambiguity inherent in human language. For example the word "wound" in English can be a noun ("I have a wound") or a verb ("He wound the clock", "He wounded me", or "The clock was wound"). The following code implements the transducer on the right, for the following parts of a dictionary: |
<pre> |
<pre> |
||
<e><p><l>wound</l><r>wound<s n="n"/><s n="sg"/></r></p></e> |
<e><p><l>wound</l><r>wound<s n="n"/><s n="sg"/></r></p></e> |
||
| Line 293: | Line 293: | ||
* Ortiz-Rojas, S., Forcada, M. L., and Ramírez-Sánchez, G. (2005) "Construcción y minimizacion eficiente de transductores de letras a partir de diccionarios con paradigmas". ''Procesamiento del Lenguaje Natural'', 35, 51–57. [http://www.sepln.org/revistaSEPLN/revista/35/07.pdf PDF] |
* Ortiz-Rojas, S., Forcada, M. L., and Ramírez-Sánchez, G. (2005) "Construcción y minimizacion eficiente de transductores de letras a partir de diccionarios con paradigmas". ''Procesamiento del Lenguaje Natural'', 35, 51–57. [http://www.sepln.org/revistaSEPLN/revista/35/07.pdf PDF] |
||
* A. Garrido-Alenda, M.L. Forcada, (2002) "Comparing nondeterministic and quasideterministic finite-state transducers built from morphological dictionaries", Procesamiento del Lenguaje Natural, (XVIII Congreso de la Sociedad Española de Procesamiento del Lenguaje Natural, Valladolid, Spain, 11-13.09.2002) [http://www.sepln.org/revistaSEPLN/revista/29/29-Pag73.pdf PDF] |
* A. Garrido-Alenda, M.L. Forcada, (2002) "Comparing nondeterministic and quasideterministic finite-state transducers built from morphological dictionaries", Procesamiento del Lenguaje Natural, (XVIII Congreso de la Sociedad Española de Procesamiento del Lenguaje Natural, Valladolid, Spain, 11-13.09.2002) [http://www.sepln.org/revistaSEPLN/revista/29/29-Pag73.pdf PDF] |
||
| − | * R.C. Carrasco, M.L. Forcada, (2002) "Incremental construction and maintenance of minimal finite-state automata", Computational Linguistics, 28:2, 207-216 [http://www.dlsi.ua.es/~mlf/docum/carrasco02j.pdf PDF] |
+ | * R.C. Carrasco, M.L. Forcada, (2002) "Incremental construction and maintenance of minimal finite-state automata", ''Computational Linguistics'', 28:2, 207-216 [http://www.dlsi.ua.es/~mlf/docum/carrasco02j.pdf PDF] |
| − | * Alicia Garrido-Alenda, Mikel L. Forcada, Rafael C. Carrasco, (2002) "Incremental construction and maintenance of morphological analysers based on augmented letter transducers", in Proceedings of TMI 2002 (Theoretical and Methodological Issues in Machine Translation, Keihanna/Kyoto, Japan, March 2002), p. 53-62 [http://www.dlsi.ua.es/~mlf/docum/garrido02p.pdf PDF] |
+ | * Alicia Garrido-Alenda, Mikel L. Forcada, Rafael C. Carrasco, (2002) "Incremental construction and maintenance of morphological analysers based on augmented letter transducers", in ''Proceedings of TMI 2002'' (Theoretical and Methodological Issues in Machine Translation, Keihanna/Kyoto, Japan, March 2002), p. 53-62 [http://www.dlsi.ua.es/~mlf/docum/garrido02p.pdf PDF] |
| − | * J. Daciuk, S. Mihov, B. W. Watson, R. E. Watson (2000). "Incremental construction of minimal acyclic finite-state automata", in Computational Linguistics, 26(1):3-16. [http://www.eti.pg.gda.pl/~jandac/incr_fst.ps.gz PS] |
+ | * J. Daciuk, S. Mihov, B. W. Watson, R. E. Watson (2000). "Incremental construction of minimal acyclic finite-state automata", in ''Computational Linguistics'', 26(1):3-16. [http://www.eti.pg.gda.pl/~jandac/incr_fst.ps.gz PS] |
[[Category:Documentation]] |
[[Category:Documentation]] |
||
Revision as of 22:14, 21 December 2011
This page intends to describe how and why the morphological dictionaries in Apertium work the way they do. Descriptions will be presented, along with examples in code. It is hoped that this will help people understand how the dictionaries work without needing to wade through pages of equations. Morphological dictionaries in Apertium (or more properly lttoolbox) are based on finite-state transducer technology; in this way they can also be referred to as lexical transducers. The task of a morphological dictionary is to model the rules that govern the internal structure of words in a language.
For example, speakers of English realise that the words "dog" and "dogs" are related, that "dogs" is to "dog" as "cats" is to "cat". The rules understood by the speaker reflect specific patterns and regularities in the way in which words are formed from smaller units and how those smaller units interact.
Finite-state transducers are not the only way to model these rules. It is also possible to write the rules in scripting languages such as perl or python, or as a lexer (examples include the Buckwalter morphological analyser for Arabic, or IceMorphy for Icelandic). There are however a number of downsides to this method:
- The analysers created are not reversible; that is, you cannot use the same model to analyse and generate.
- As the rule content may be both imperative and declarative, programs can be more complicated for non-experts to understand and edit.
In contrast, finite-state transducers are both reversible (the same description can be used for both analysis and generation) and declarative (a description of the morphological rules is separate from the algorithm which processes them). Note that analysers may also be described as decorated tries or finite-state acceptors (for example hunmorph); this may be declarative but non-reversible (i.e. not applicable to generation).
Finite-state automata
To start with, it is worth defining a finite-state automaton and how the two main types differ. This will not be an exhaustive description, just an overview so that the difference can be distinguished for the purposes of this article. To begin with, some terminology; if you are familiar with graphs (as in the data structure), this might help. A finite-state automaton can be visualised as a graph, with the nodes representing states and the arcs representing transitions.
Acceptors
A finite-state acceptor (or recogniser), as seen to the right, is an automaton which accepts or rejects input strings. Taking the example at the right, we can see the automaton has:
- a number of possible input characters, or alphabet (the characters 'b', 'e' and 'r'), denoted as
- a start state; in formal definitions this is usually labelled
- a number of intermediate states, often denoted by
- two final states, denoted by
- a number of transitions
We can crudely emulate this in a programming language such as python in order to get an idea of the behaviour of these automata.
states = ['b', 'e', 'e', 'r']; # Set of states
current_state = 0; # Set current state to start state
c = sys.stdin.read(1);
while c: # Input loop
if current_state == len(states): # If we've reached the final state
sys.stdout.write('Yes');
sys.exit(0);
elif c == states[current_state]: # If the input matches the value of the current state
current_state += 1;
else: # If the input does not match the current state and we're not final
sys.stdout.write('No');
sys.exit(1);
c = sys.stdin.read(1);
When the input on stdin is "beer", output yes; otherwise output no,
$ echo "beer" | python fsa.py Yes $ echo "bee" | python fsa.py No
It is worth noting that a finite-state acceptor can accept any string that can be defined by a regular expression. For example, if we want to accept the expression bee*r, which can also be written be+r — that is, "b" followed by one or more "e" followed by "r" (e.g. ber, beer, beeer, ...) — we could do it with a finite-state acceptor. Finite-state acceptors can be used in applications such as spell-checking, where one of the basic tasks is to check if a word exists or not in a list of words. Using an acceptor is more efficient than the equivalent list, for reasons which will be outlined below.
- fill in more formal stuff here
Transducers
Whilst acceptors are useful, for morphological analysis we need something that will give us an output for a given input. For example, given a surface form of a word, it will give us the lexical form (analysis); or given the lexical form, it will give us the surface form (generation). For this, we need a transducer. A transducer is very much like an acceptor, with this main difference: instead of each transition consuming a character from the input, each transition consumes a character and outputs a character. So instead of having a symbol on each arc, we have a tuple, input and output (see diagram to the right).
The diagram to the right shows a finite-state transducer[1] for the strings "beer" and "beers". This transducer has:
- an input alphabet, (the characters 'b', 'e', 'r' and 's')
- an output alphabet, (the characters 'b', 'e', 'r' and the multi-character symbols
<n>,<sg>and<pl>) - a start state,
- a number of intermediate states,
- a set of final states,
- a number of transitions
Note how in the diagram, the "non-accepting" state (no) has been left out.
Again, we can emulate this transducer with some python code:
transitions = {(0,'b'):1, (1,'e'):2, (2,'e'):3, (3,'r'):4, (4,''):5, (4,'s'):6, (5,''):7, (6,''):7};
states = {0:'b', 1:'e', 2:'e', 3:'r', 4:'<n>', 5:'<sg>', 6:'<pl>', 7:''};
current_state = 0; # Start state
def step(state, symbol): # The current state and input symbol
sys.stdout.write(states[state]); # Print the output symbol of the transition
return transitions[(state, symbol)]; # Return the next state
c = sys.stdin.read(1);
while states[current_state] != '': # While we aren't in a final state
current_state = step(current_state, c); # Step to the next state
c = sys.stdin.read(1).replace('\n', '');
$ echo "beer" | python fst.py beer<n><sg> $ echo "beers" | python fst.py beer<n><pl>
Determinism
The above transducer is deterministic; that is, for any given state and input symbol, it can only pass on to one state, or accept. In contrast, a non-deterministic transducer (as on the right) is one which from a given state and input symbol can branch to more than one state. That is, it can take more than one path through the transducer simultaneously. Note that although the transducer on the right branches, it branches in a deterministic way; after consuming the string "beer", it can either step to (s:<n>) if the next input symbol is 's', or (θ:<n>) otherwise.
A non-deterministic finite-state transducer is modelled as:
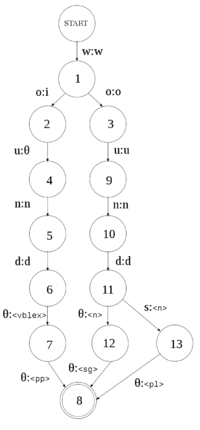
The benefit of non-deterministic transducers over deterministic transducers is that they allow us to capture the ambiguity inherent in human language. For example the word "wound" in English can be a noun ("I have a wound") or a verb ("He wound the clock", "He wounded me", or "The clock was wound"). The following code implements the transducer on the right, for the following parts of a dictionary:
<e><p><l>wound</l><r>wound<s n="n"/><s n="sg"/></r></p></e> <e><p><l>wounds</l><r>wound<s n="n"/><s n="pl"/></r></p></e> <e><p><l>wound</l><r>wind<s n="vblex"/><s n="pp"/></r></p></e>
states = set([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]);
transitions = {
(0,'w'):[('w',1)],
(1,'o'):[('i',2), ('o',3)],
(2,'u'):[('',4)], (4,'n'):[('n',5)], (5,'d'):[('d',6)], (6,''):[('<vblex>',7)], (7,''):[('<pp>',8)],
(3,'u'):[('u',9)], (9,'n'):[('n',10)], (10,'d'):[('d',11)],
(11,''):[('<n>',12)],
(11,'s'):[('<n>',13)],
(12,''):[('<sg>',8)],
(13,''):[('<pl>',8)]
};
initial_state = 0;
accepting_states = set([8]);
current_states = set([initial_state]); # Set containing the set of current states
state_output_pairs = {}; # A structure to contain the list of "alive state-output pairs"
state_output_pairs[0] = set([('', 0)]);
accepting_output_pairs = set(); # The set of state-output pairs that are accepting
input = c = sys.stdin.read(1);
def closure(S, reached_states): # Calculate epsilon closure over state S
global state_output_pairs;
if S not in state_output_pairs:
state_output_pairs[S] = set();
if (S, '') in transitions:
for state in transitions[(S, '')]:
reached_states.add(state[1]);
if state[1] not in state_output_pairs:
state_output_pairs[state[1]] = set();
for pair in state_output_pairs[S]:
state_output_pairs[state[1]].add((pair[0] + state[0], state[1]));
closure(state[1], reached_states);
return reached_states;
def step(S, c): # Step the transducer
global accepting_states, state_output_pairs;
reached_states = set();
if S in accepting_states:
return set([S]);
if (S, c) in transitions:
for state in transitions[(S, c)]:
closure(state[1], reached_states);
reached_states.add(state[1]);
if state[1] not in state_output_pairs:
state_output_pairs[state[1]] = set();
for pair in state_output_pairs[S]:
state_output_pairs[state[1]].add((pair[0] + state[0], state[1]));
closure(state[1], reached_states);
return reached_states;
while c != '': # Loop until no input remains
reached_states = set();
for state in current_states:
if state not in state_output_pairs:
state_output_pairs[state] = set();
reached_states |= step(state, c);
del state_output_pairs[state];
current_states = reached_states;
c = sys.stdin.read(1).replace('\n','');
input += c;
print('^' + '/'.join([input] + [analysis[0] for analysis in state_output_pairs[8]]) + '$')
$ echo "wound" | python nfst.py ^wound/wind<vblex><pp>/wound<n><sg>$ $ echo "wounds" | python nfst.py ^wounds/wound<n><pl>$
A nice exercise might be to extend the state/transition structures to add the missing analyses.
Determinisation
Minimisation
Subsequential transducers
-Subsequential transducers
Application
Paradigms
<pardef n="-s">
<e>
<p>
<l/>
<r><s n="n"/><s n="sg"/></r>
</p>
</e>
<e>
<p>
<l>s</l>
<r><s n="n"/><s n="pl"/></r>
</p>
</e>
</pardef>
Sections
- Standard
- Inconditional section
- See also: Inconditional section
- Postblank
- Preblank
Entries
Behaviour
- Determinism
- Minimisation
- Tokenisation
Terminology
- string
- alphabet
- symbol
- empty string
See also
Notes
- ↑ In particular this is a "letter transducer"; that is, each transition is modelled as an arc between two letters in the alphabet
Further reading
- Ortiz-Rojas, S., Forcada, M. L., and Ramírez-Sánchez, G. (2005) "Construcción y minimizacion eficiente de transductores de letras a partir de diccionarios con paradigmas". Procesamiento del Lenguaje Natural, 35, 51–57. PDF
- A. Garrido-Alenda, M.L. Forcada, (2002) "Comparing nondeterministic and quasideterministic finite-state transducers built from morphological dictionaries", Procesamiento del Lenguaje Natural, (XVIII Congreso de la Sociedad Española de Procesamiento del Lenguaje Natural, Valladolid, Spain, 11-13.09.2002) PDF
- R.C. Carrasco, M.L. Forcada, (2002) "Incremental construction and maintenance of minimal finite-state automata", Computational Linguistics, 28:2, 207-216 PDF
- Alicia Garrido-Alenda, Mikel L. Forcada, Rafael C. Carrasco, (2002) "Incremental construction and maintenance of morphological analysers based on augmented letter transducers", in Proceedings of TMI 2002 (Theoretical and Methodological Issues in Machine Translation, Keihanna/Kyoto, Japan, March 2002), p. 53-62 PDF
- J. Daciuk, S. Mihov, B. W. Watson, R. E. Watson (2000). "Incremental construction of minimal acyclic finite-state automata", in Computational Linguistics, 26(1):3-16. PS