Dictionnaire morphologique

In English

Cette page a pour but de décrire comment et pourquoi les dictionnaires morphologiques travaillent dans Apertium de la manière dont ils le font. Les descriptions seront présentées, avec des exemples de code. On espère que ça aidera les gens à comprendre comment les dictionnaires travaillent sans avoir besoin de parcourir des pages d'équations. Les dictionnaires morphologiques dans Apertium (ou plus précisément lttoolbox) sont basés sur la technologie des transducteurs à états finis, de cette manière ils peuvent aussi être appelés transducteurs lexicaux. La tâche d'un dictionnaire morphologique est de modéliser les règles qui régissent la structure interne des mots dans une langue.

Par exemple, les francophones se rendent compte que les mots "chien" et "chiens" sont liés, et que "chiens" est à "chien" ce que "chats" est à "chat". Les règles comprises par le locuteur reflètent des modèles spécifiques et des régularités dans la manière dont les mots sont formés depuis les plus petites unités et comment ces plus petites unités interagissent.

Les transducteurs à états finis ne sont pas la seule manière de modéliser ces règles, il est également possible d'écrire les règles en langage script comme Perl ou Python, ou comme un lexer(?) (exemples dans l'analyseur morphologique Buckwalter pour l'arabe ou IceMorphy pour l'islandais). Il y a cependant un certain nombre de désavantages à cette méthode :

Les analyseurs créés ne sont pas réversibles, c'est à dire que vous ne pouvez pas utiliser le même modèle pour analyser et générer.
Comme le contenu des règles peut être aussi bien impératif que déclaratif, les programmes peuvent être plus compliqués à comprendre et à éditer par des non-experts.

Au contraire, les transducteurs à états finis sont :

réversibles: la même description peut être utilisée pour l'analyse et pour la génération;
déclaratifs, en ce sens qu'une description de règles morphologiques est écrite séparément de l'algorithme qui les traite.

Notez que les analyseurs peuvent aussi être décrits comme des essais(?) décorés, ou des accepteurs à états finis (par exemple hunmorph), cela peut être déclaratif, mais non réversible (par exemple inutilisable pour la génération).

Un accepteur à états finis pour la chaîne "beer".

Automate à états finis

Pour commencer il est utile de définir ce qu'est un automate à états finis, et comment les deux types principaux diffèrent. Ce ne sera pas une description exhaustive, juste un aperçu afin que la différence puisse être distinguée pour l'objet de cet article. Pour commencer, quelque terminologie, si vous êtes familier avec les graphes (comme en structure de données) cela pourrait aider. Un automate à états finis peut être visualisé comme un graphe, avec les noeuds représentant les états, et les arcs représentant les transitions.

Accepteurs

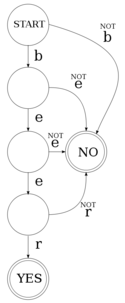
Un accepteur à états finis (ou recogniser), comme vu dans l'image à droite, est un automate qui accepte ou rejette des chaînes en entrée. Donc, en prenant l'exemple de droite, on peut voir que l'automate a :

un certain nombre de caractères d'entrée possibles, ou un alphabet (les caractères 'b', 'e' et 'r'), sont notés $\Sigma$
un état de départ, dans les définitions formelles c'est habituellement marqué $s_{0}$
un certain nombre d'états intermédiaires, souvent notés $S$
deux états finaux, notés $F$
un certain nombre de transitions

Nous pouvons émuler cela grossièrement dans un langage de programmation comme Python afin de se faire une idée du comportement de ces automates.

states = ['b', 'e', 'e', 'r']; # Initialiser les états
current_state = 0;             # Initialiser l'états courant comme état de départ

c = sys.stdin.read(1);

while c:                       # Boucle d'entrée
        if current_state == len(states): # Si on a atteint un état final
                sys.stdout.write('Yes');
                sys.exit(0);
        elif c == states[current_state]: # Si l'entrée correspond à la valeur de l'état courant
                current_state += 1;
        else:                            # Si l'entrée ne correspond pas à l'état courant et on n'est pas à l'état final
                sys.stdout.write('No');
                sys.exit(1);

        c = sys.stdin.read(1);

Lorsque l'entrée stdin est "beer", la sortie est yes, sinon la sortie est no,

Cet accepteur à états finis va accepter chaque chaîne définie par l'expression régulière be*r, c'est à dire br, ber, beer, beeer, beeeer, ...

$ echo "beer" | python fsa.py
Yes

$ echo "bee" | python fsa.py
No

Il est utile de noter qu'un accepteur à états finis peut accepter toute chaîne qui peut être définie par une expression régulière. Par exemple, si on veut accepter l'expression bee*r, qu'on peut écrire aussi be+r c'est à dire un "b" suivi d'un ou plusieurs"e" suivi par un "r" (ex: ber, beer, beeer, ...), on pourrait le faire avec un accepteur à états finis. Les accepteurs à états finis peuvent être utilisés dans des applications comme des correcteurs orthographiques, lorsqu'une tâche de base consiste à vérifier si un mot existe ou pas dans une liste de mots. Utiliser un accepteur est plus efficace que la liste équivalente pour les raisons qui vont être décrites plus loin.

à compléter ici

Transducteurs

Un transducteur à états finis pour les chaînes "beer" et "beers", la sortie est le lemme du mot, "beer", la partie de discours, <n> pour "nom" et ensuite le nombre, soit singulier (<sg>) soit pluriel (<pl>).

Bien que les accepteurs soient utiles, pour l'analyse morphologique nous avons besoin de quelque-chose qui va nous donner une sortie pour une entrée donnée. Par exemple, à partir de la forme de surface d'un mot, il nous donnera la forme lexicale (analyse) ou à partir de la forme lexicale il nous donnera la forme de surface (génération). Pour cela, on a besoin d'un transducteur. Un transducteur est très semblable à un accepteur, avec comme principale différence qu'au lieu de consommer un caractère d'entrée à chaque transition, chaque transition consomme un caractère et génère un caractère. Donc au lieu d'avoir un symbole sur chaque arc, on a un tuple, entrée et sortie (voir le diagramme de droite).

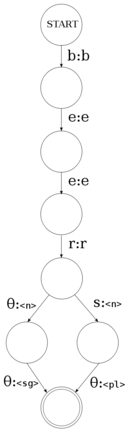
Le diagramme de droite montre un transducteur à états finis^[1] pour les chaînes "beer" et "beers", ce transducteur a :

un alphabet d'entrée, $\Sigma$ (les caractères 'b', 'e', 'r' et 's')
un alphabet de sortie, $\Gamma$ (les caractères 'b', 'e', 'r' et les symboles multi-caractères <n>, <sg> et <pl>)
un état de départ, $s_{0}$
un certain nombre d'états intermédiaires, $S$
un ensemble d'états finaux, $F$
un certain nombre de transitions

Notez que dans le diagramme, les états "non acceptés" (no) ont été laissés de coté.

De nouveau, on peut émuler ce transducteur avec un peu de code Python :

transitions = {(0,'b'):1, (1,'e'):2, (2,'e'):3, (3,'r'):4, (4,''):5, (4,'s'):6, (5,''):7, (6,''):7};
states = {0:'b', 1:'e', 2:'e', 3:'r', 4:'<n>', 5:'<sg>', 6:'<pl>', 7:''};

current_state = 0; # État de départ

def step(state, symbol): # L'état courant et le symbole d'entrée
        sys.stdout.write(states[state]); # Écrire le symbole de sortie de la transition
        return transitions[(state, symbol)]; # Retourner l'état suivant

c = sys.stdin.read(1);
while states[current_state] != '': # Tant qu'on n'est pas dans l'état final
        current_state = step(current_state, c); # Passer à l'état suivant

        c = sys.stdin.read(1).replace('\n', '');

$ echo "beer" | python fst.py 
beer<n><sg>

$ echo "beers" | python fst.py 
beer<n><pl>

Déterminisme

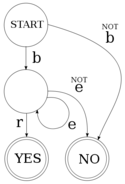
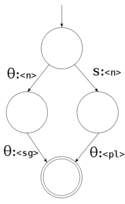
Un transducteur à états finis non déterministe pour trois chaînes : wound, wound, wounds.

Le transducteur du dessus est déterministe, ce qui veut dire que pour chaque état et symbole d'entrée donnés il peut seulement passer à un autre état, ou accepter. Au contraire, un transducteur non déterministe (comme à droite) est l'un de ceux pour lesquels à partir d'un état et un symbole d'entrée donnés on peut se ramifier vers plusieurs états. C'est à dire qu'il peut prendre simultanément plus d'un chemin à travers le transducteur. Notez que le transducteur ci-dessus, se ramifie de manière déterministe, après avoir consommé la chaîne "beer", il peut aussi bien aller vers (s:<n>) si le prochain symbole d'entrée est 's', ou vers (θ:<n>) dans l'autre cas.

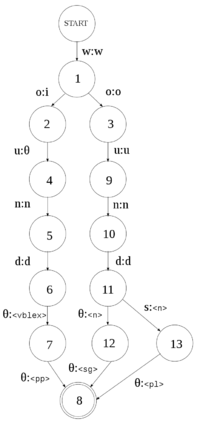
Un transducteur à états finis non déterministe est modélisée comme :

L'avantage des transducteurs non déterministes sur les transducteurs déterministes est qu'ils nous permettent de saisir l'ambiguïté inhérente à un langage humain. Par exemple le mot "wound" en anglais peut être un nom "I have a wound" (j'ai une blessure), un verbe "He wound the clock" (traduction ?), "He wounded me" (il m'a blessé) ou "The clock was wound" (traduction ?). Les codes qui suivent implémentent le transducteurs de droite, pour les parties qui suivent d'un dictionnaire :

	<e><p><l>wound</l><r>wound<s n="n"/><s n="sg"/></r></p></e>
	<e><p><l>wounds</l><r>wound<s n="n"/><s n="pl"/></r></p></e>
	<e><p><l>wound</l><r>wind<s n="vblex"/><s n="pp"/></r></p></e>

states = set([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]);

transitions = {
        (0,'w'):[('w',1)],
        (1,'o'):[('i',2), ('o',3)],
        (2,'u'):[('',4)], (4,'n'):[('n',5)], (5,'d'):[('d',6)], (6,''):[('<vblex>',7)], (7,''):[('<pp>',8)],
        (3,'u'):[('u',9)], (9,'n'):[('n',10)], (10,'d'):[('d',11)], 

        (11,''):[('<n>',12)], 
        (11,'s'):[('<n>',13)],

        (12,''):[('<sg>',8)],
        (13,''):[('<pl>',8)]
};

initial_state = 0;
accepting_states = set([8]);
current_states = set([initial_state]); # Ensemble contenant l'ensemble des états courants
state_output_pairs = {};               # Une structure pour contenir la liste des "paires de sortie d'états vivants" 
state_output_pairs[0] = set([('', 0)]); 
accepting_output_pairs = set();        # L'ensemble des paires de sortie d'états acceptées

input = c = sys.stdin.read(1);

def closure(S, reached_states):        # Calculer la fermeture epsilon (?) après l'état S
        global state_output_pairs;

        if S not in state_output_pairs:
                state_output_pairs[S] = set();

        if (S, '') in transitions:
                for state in transitions[(S, '')]:
                        reached_states.add(state[1]);

                        if state[1] not in state_output_pairs:
                                state_output_pairs[state[1]] = set();

                        for pair in state_output_pairs[S]:
                                state_output_pairs[state[1]].add((pair[0] + state[0], state[1]));

                        closure(state[1], reached_states);

        return reached_states;

def step(S, c):                        # Step the transducer
        global accepting_states, state_output_pairs;
        reached_states = set();

        if S in accepting_states:
                return set([S]);

        if (S, c) in transitions: 
                for state in transitions[(S, c)]:
                        closure(state[1], reached_states);
                        reached_states.add(state[1]);

                        if state[1] not in state_output_pairs:
                                state_output_pairs[state[1]] = set();

                        for pair in state_output_pairs[S]:
                                state_output_pairs[state[1]].add((pair[0] + state[0], state[1]));

                        closure(state[1], reached_states);

        return reached_states;

while c != '':                        # Boucle jusqu'à ce qu'il ne reste plus d'entrée
        reached_states = set();

        for state in current_states:
                if state not in state_output_pairs:
                        state_output_pairs[state] = set();
                reached_states |= step(state, c);
                del state_output_pairs[state];

        current_states = reached_states;

        c = sys.stdin.read(1).replace('\n','');
        input += c;

print('^' + '/'.join([input] + [analysis[0] for analysis in state_output_pairs[8]]) + '$')

$ echo "wound" | python nfst.py 
^wound/wind<vblex><pp>/wound<n><sg>$

$ echo "wounds" | python nfst.py 
^wounds/wound<n><pl>$

Un bel exercice pourrait être d'étendre les structures état/transition pour ajouter les analyses manquantes.

Déterminisation

Minimisation

Transducteurs subséquentiels

$p$ -transducteurs subséquentiels

Application

Un transducteur pour paradigme du pluriel régulier -s en anglais, français, ... Les transducteurs générés depuis des paradigmes peuvent être réutilisés.

Paradigmes

  <pardef n="-s">
    <e>
      <p>
        <l/>
        <r><s n="n"/><s n="sg"/></r>
      </p>
    </e>  
    <e>
      <p>
        <l>s</l>
        <r><s n="n"/><s n="pl"/></r>
      </p>
    </e>
  </pardef>

Sections

Standard

Inconditional section

Voir aussi : Section inconditionnelle

Postblank

Preblank

Entrées

Comportement

Déterminisme
Minimisation
Tokenisation

Terminologie

chaîne
alphabet
symbole
chaîne vide

Voir aussi

Bases sur les dictionnaires unilingues

Notes

↑ En particulier c'est un "transducteur de lettres", qui à chaque transition est modélisé comme entre deux lettres dans l'alphabet

Lectures complémentaires

Ortiz-Rojas, S., Forcada, M. L., and Ramírez-Sánchez, G. (2005) "Construcción y minimizacion eﬁciente de transductores de letras a partir de diccionarios con paradigmas". Procesamiento del Lenguaje Natural, 35, 51–57. PDF
A. Garrido-Alenda, M.L. Forcada, (2002) "Comparing nondeterministic and quasideterministic transducteurs à états finis built from dictionnaires morphologiques", Procesamiento del Lenguaje Natural, (XVIII Congreso de la Sociedad Española de Procesamiento del Lenguaje Natural, Valladolid, Spain, 11-13.09.2002) PDF
R.C. Carrasco, M.L. Forcada, (2002) "Incremental construction and maintenance of minimal finite-state automata", Computational Linguistics, 28:2, 207-216 PDF
Alicia Garrido-Alenda, Mikel L. Forcada, Rafael C. Carrasco, (2002) "Incremental construction and maintenance of morphological analysers based on augmented letter transducers", in Proceedings of TMI 2002 (Theoretical and Methodological Issues in Machine Translation, Keihanna/Kyoto, Japan, March 2002), p. 53-62 PDF
J. Daciuk, S. Mihov, B. W. Watson, R. E. Watson (2000). "Incremental construction of minimal acyclic finite-state automata", in Computational Linguistics, 26(1):3-16. PS

[1] En particulier c'est un "transducteur de lettres", qui à chaque transition est modélisé comme entre deux lettres dans l'alphabet

[1]

Dictionnaire morphologique

Contents

Automate à états finis

Accepteurs

Transducteurs

Déterminisme

Déterminisation

Minimisation

Transducteurs subséquentiels

$p$ -transducteurs subséquentiels

Application

Paradigmes

Sections

Entrées

Comportement

Terminologie

Voir aussi

Notes

Lectures complémentaires

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Tools

Dictionnaire morphologique

Contents

Automate à états finis

Accepteurs

Transducteurs

Déterminisme

Déterminisation

Minimisation

Transducteurs subséquentiels

p {\displaystyle p} -transducteurs subséquentiels

Application

Paradigmes

Sections

Entrées

Comportement

Terminologie

Voir aussi

Notes

Lectures complémentaires

Navigation menu

Search

$p$ -transducteurs subséquentiels