Morphological dictionary

This page intends to describe how and why the morphological dictionaries in Apertium work the way they do. Descriptions will be presented, along with examples in code. It is hoped that this will help people understand how the dictionaries work without needing to wade through pages of equations. Morphological dictionaries in Apertium (or more properly lttoolbox) are based on finite-state transducer technology; in this way they can also be referred to as lexical transducers. The task of a morphological dictionary is to model the rules that govern the internal structure of words in a language.

For example, speakers of English realise that the words "dog" and "dogs" are related, that "dogs" is to "dog" as "cats" is to "cat". The rules understood by the speaker reflect specific patterns and regularities in the way in which words are formed from smaller units and how those smaller units interact.

Finite-state transducers are not the only way to model these rules. It is also possible to write the rules in scripting languages such as perl or python, or as a lexer (examples include the Buckwalter morphological analyser for Arabic, or IceMorphy for Icelandic). There are however a number of downsides to this method:

The analysers created are not reversible; that is, you cannot use the same model to analyse and generate.
As the rule content may be both imperative and declarative, programs can be more complicated for non-experts to understand and edit.

In contrast, finite-state transducers are both reversible (the same description can be used for both analysis and generation) and declarative (a description of the morphological rules is separate from the algorithm which processes them). Note that analysers may also be described as decorated tries or finite-state acceptors (for example hunmorph); this may be declarative but non-reversible (i.e. not applicable to generation).

A finite-state acceptor for the string "beer".

Finite-state automata

To start with, it is worth defining a finite-state automaton and how the two main types differ. This will not be an exhaustive description, just an overview so that the difference can be distinguished for the purposes of this article. To begin with, some terminology; if you are familiar with graphs (as in the data structure), this might help. A finite-state automaton can be visualised as a graph, with the nodes representing states and the arcs representing transitions.

Acceptors

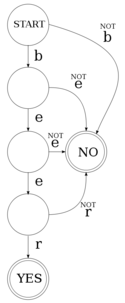
A finite-state acceptor (or recogniser), as seen to the right, is an automaton which accepts or rejects input strings. Taking the example at the right, we can see the automaton has:

a number of possible input characters, or alphabet (the characters 'b', 'e' and 'r'), denoted as $\Sigma$
a start state; in formal definitions this is usually labelled $s_{0}$
a number of intermediate states, often denoted by $S$
two final states, denoted by $F$
a number of transitions

We can crudely emulate this in a programming language such as python in order to get an idea of the behaviour of these automata.

states = ['b', 'e', 'e', 'r']; # Set of states
current_state = 0;             # Set current state to start state 

c = sys.stdin.read(1);

while c:                       # Input loop
        if current_state == len(states): # If we've reached the final state
                sys.stdout.write('Yes');
                sys.exit(0);
        elif c == states[current_state]: # If the input matches the value of the current state
                current_state += 1;
        else:                            # If the input does not match the current state and we're not final
                sys.stdout.write('No');
                sys.exit(1);

        c = sys.stdin.read(1);

When the input on stdin is "beer", output yes; otherwise output no,

This finite-state acceptor will accept any string defined by the regular expression be*r, i.e. br, ber, beer, beeer, beeeer, ...

$ echo "beer" | python fsa.py
Yes

$ echo "bee" | python fsa.py
No

It is worth noting that a finite-state acceptor can accept any string that can be defined by a regular expression. For example, if we want to accept the expression bee*r, which can also be written be+r — that is, "b" followed by one or more "e" followed by "r" (e.g. ber, beer, beeer, ...) — we could do it with a finite-state acceptor. Finite-state acceptors can be used in applications such as spell-checking, where one of the basic tasks is to check if a word exists or not in a list of words. Using an acceptor is more efficient than the equivalent list, for reasons which will be outlined below.

fill in more formal stuff here

Transducers

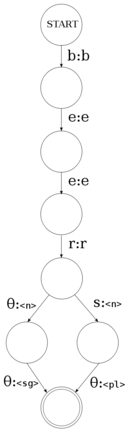
A finite-state transducer for the strings "beer" and "beers"; the output is the lemma of the word, "beer", the part-of-speech, <n> for "noun" and then the number, either singular (<sg>) or plural (<pl>).

Whilst acceptors are useful, for morphological analysis we need something that will give us an output for a given input. For example, given a surface form of a word, it will give us the lexical form (analysis); or given the lexical form, it will give us the surface form (generation). For this, we need a transducer. A transducer is very much like an acceptor, with this main difference: instead of each transition consuming a character from the input, each transition consumes a character and outputs a character. So instead of having a symbol on each arc, we have a tuple, input and output (see diagram to the right).

The diagram to the right shows a finite-state transducer^[1] for the strings "beer" and "beers". This transducer has:

an input alphabet, $\Sigma$ (the characters 'b', 'e', 'r' and 's')
an output alphabet, $\Gamma$ (the characters 'b', 'e', 'r' and the multi-character symbols <n>, <sg> and <pl>)
a start state, $s_{0}$
a number of intermediate states, $S$
a set of final states, $F$
a number of transitions

Note how in the diagram, the "non-accepting" state (no) has been left out.

Again, we can emulate this transducer with some python code:

transitions = {(0,'b'):1, (1,'e'):2, (2,'e'):3, (3,'r'):4, (4,''):5, (4,'s'):6, (5,''):7, (6,''):7};
states = {0:'b', 1:'e', 2:'e', 3:'r', 4:'<n>', 5:'<sg>', 6:'<pl>', 7:''};

current_state = 0; # Start state

def step(state, symbol): # The current state and input symbol
        sys.stdout.write(states[state]); # Print the output symbol of the transition
        return transitions[(state, symbol)]; # Return the next state

c = sys.stdin.read(1);
while states[current_state] != '': # While we aren't in a final state
        current_state = step(current_state, c); # Step to the next state

        c = sys.stdin.read(1).replace('\n', '');

$ echo "beer" | python fst.py 
beer<n><sg>

$ echo "beers" | python fst.py 
beer<n><pl>

Determinism

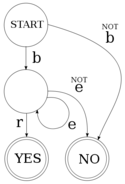
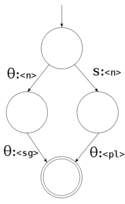
A non-deterministic finite-state transducer for three strings: wind, wound, wounds.

The above transducer is deterministic; that is, for any given state and input symbol, it can only pass on to one state, or accept. In contrast, a non-deterministic transducer (as on the right) is one which from a given state and input symbol can branch to more than one state. That is, it can take more than one path through the transducer simultaneously. Note that although the transducer on the right branches, it branches in a deterministic way; after consuming the string "beer", it can either step to (s:<n>) if the next input symbol is 's', or (θ:<n>) otherwise.

A non-deterministic finite-state transducer is modelled as:

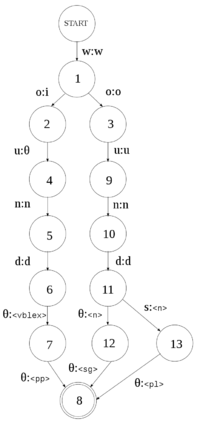
The benefit of non-deterministic transducers over deterministic transducers is that they allow us to capture the ambiguity inherent in human language. For example the word "wound" in English can be a noun ("I have a wound") or a verb ("He wound the clock", "He wounded me", or "The clock was wound"). The following code implements the transducer on the right, for the following parts of a dictionary:

	<e><p><l>wound</l><r>wound<s n="n"/><s n="sg"/></r></p></e>
	<e><p><l>wounds</l><r>wound<s n="n"/><s n="pl"/></r></p></e>
	<e><p><l>wound</l><r>wind<s n="vblex"/><s n="pp"/></r></p></e>

states = set([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]);

transitions = {
        (0,'w'):[('w',1)],
        (1,'o'):[('i',2), ('o',3)],
        (2,'u'):[('',4)], (4,'n'):[('n',5)], (5,'d'):[('d',6)], (6,''):[('<vblex>',7)], (7,''):[('<pp>',8)],
        (3,'u'):[('u',9)], (9,'n'):[('n',10)], (10,'d'):[('d',11)], 

        (11,''):[('<n>',12)], 
        (11,'s'):[('<n>',13)],

        (12,''):[('<sg>',8)],
        (13,''):[('<pl>',8)]
};

initial_state = 0;
accepting_states = set([8]);
current_states = set([initial_state]); # Set containing the set of current states
state_output_pairs = {};               # A structure to contain the list of "alive state-output pairs" 
state_output_pairs[0] = set([('', 0)]); 
accepting_output_pairs = set();        # The set of state-output pairs that are accepting

input = c = sys.stdin.read(1);

def closure(S, reached_states):        # Calculate epsilon closure over state S
        global state_output_pairs;

        if S not in state_output_pairs:
                state_output_pairs[S] = set();

        if (S, '') in transitions:
                for state in transitions[(S, '')]:
                        reached_states.add(state[1]);

                        if state[1] not in state_output_pairs:
                                state_output_pairs[state[1]] = set();

                        for pair in state_output_pairs[S]:
                                state_output_pairs[state[1]].add((pair[0] + state[0], state[1]));

                        closure(state[1], reached_states);

        return reached_states;

def step(S, c):                        # Step the transducer
        global accepting_states, state_output_pairs;
        reached_states = set();

        if S in accepting_states:
                return set([S]);

        if (S, c) in transitions: 
                for state in transitions[(S, c)]:
                        closure(state[1], reached_states);
                        reached_states.add(state[1]);

                        if state[1] not in state_output_pairs:
                                state_output_pairs[state[1]] = set();

                        for pair in state_output_pairs[S]:
                                state_output_pairs[state[1]].add((pair[0] + state[0], state[1]));

                        closure(state[1], reached_states);

        return reached_states;

while c != '':                        # Loop until no input remains
        reached_states = set();

        for state in current_states:
                if state not in state_output_pairs:
                        state_output_pairs[state] = set();
                reached_states = reached_states.union(step(state, c));
                del state_output_pairs[state];

        current_states = reached_states;

        c = sys.stdin.read(1).replace('\n','');
        input += c;

accepting_output_pairs = list(state_output_pairs[8]);

sys.stdout.write('^' + input + '/');
for count, analysis in enumerate(accepting_output_pairs):
        if count == len(accepting_output_pairs) - 1:
                sys.stdout.write(analysis[0] + '$\n');
        else:
                sys.stdout.write(analysis[0] + '/');

$ echo "wound" | python nfst.py 
^wound/wind<vblex><pp>/wound<n><sg>$

$ echo "wounds" | python nfst.py 
^wounds/wound<n><pl>$

A nice exercise might be to extend the state/transition structures to add the missing analyses.

Determinisation

Minimisation

Subsequential transducers

$p$ -Subsequential transducers

Application

A transducer for the regular -s plural paradigm in English. Transducers generated from paradigms can be re-used.

Paradigms

  <pardef n="-s">
    <e><p><l/><r><s n="n"/><S n="sg"/></r></p></e>
    <e><p><l>s</l><r><s n="n"/><S n="sg"/></r></p></e>
  </pardef>

Sections

Standard

Inconditional section: See also: Inconditional section

Postblank

Preblank

Entries

Behaviour

Determinism
Minimisation
Tokenisation

Terminology

string
alphabet
symbol
empty string

Notes

↑ In particular this is a "letter transducer"; that is, each transition is modelled as an arc between two letters in the alphabet

Morphological dictionary

Contents

Finite-state automata

Acceptors

Transducers

Determinism

Determinisation

Minimisation

Subsequential transducers

$p$ -Subsequential transducers

Application

Paradigms

Sections

Entries

Behaviour

Terminology

See also

Notes

Further reading

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Tools

Morphological dictionary

Contents

Finite-state automata

Acceptors

Transducers

Determinism

Determinisation

Minimisation

Subsequential transducers

p {\displaystyle p} -Subsequential transducers

Application

Paradigms

Sections

Entries

Behaviour

Terminology

See also

Notes

Further reading

Navigation menu

Search

$p$ -Subsequential transducers