Talk:Automatically trimming a monodix
Contents
Implementing automatic trimming in lttoolbox
The current method: compile the analyser in the normal way, then lt-trim loads it and loops through all its states, trying to do the same steps in parallel with the compiled bidix:
trim(current_a, current_b):
for symbol, next_a in analyser.transitions[current_a]:
found = false
for s, next_b in bidix.transitions[current_b]:
if s==symbol:
trim(next_a, next_b)
found = true
if seen tags:
found = true
if !found && !current_b.isFinal():
delete symbol from analyser.transitions[current_a]
// else: all transitions from this point on will just be carried over unchanged by bidix
trim(analyser.initial, bidix.initial)
Trimming while reading the XML file might have lower memory usage, but seems like more work, since pardefs are read before we get to an "initial" state.
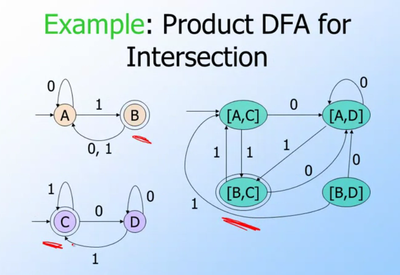
A slightly different approach is to create the product automaton for intersection, marking as final only state-pairs where both parts of the state-pair are final in the original automata. Minimisation should remove unreachable state-pairs. However, this quickly blows up in memory usage since it creates all possible state pairs first (cartesian product), not just the useful ones.
https://github.com/unhammer/lttoolbox/branches has some experiments, see e.g. branches product-intersection and df-intersection
TODO
- Would it make things faster if we first clear out the right-sides of the bidix and minimize that?
- remove all those ifdef DEBUG's and wcerr's
- more tests?
- if no objections: git svn dcommit
#-type multiwords
The implementation: first "preprocess" (in memory) the bidix FST so it has the same format as the analyser, ie. instead of "take# out<vblex>" it has "take<vblex># out".
Say you have these entries in the bidix:
take# out<vblex> take# out<n> take# in<vblex> take<n> take<vblex>
We do a depth-first traversal, and then after reading all of "take", we see t=transition(A, B, ε, #). We remove that transition, and instead add the result of copyWithTagsFirst(t), which returns a new transducer that represents these partial analyses:
<vblex># out <n># out <vblex># in
pseudocode
def moveLemqsLast()
new_t = Transducer()
seen = set()
todo = [initial]
while todo:
src = todo.pop()
for left, right, trg in transitions[src]:
if left == '#':
new_t.transitions[src][epsilon].insertTransducer( copyWithTagsFirst(trg) )
else:
new_t.linkStates(src, trg, left, right)
if trg not in seen:
todo.push(trg)
seen.insert(trg)
return new_t
def copyWithTagsFirst(start):
seen = set()
new_t = Transducer()
lemq = Transducer()
# not shown below since it's quite trivial: states in new_t/lemq will get
# different indices from corresponding states in this, so we need to record
# those correspondences in a table in order to use the right one:
states_this_new = { start: new_t.initial }
states_this_lemq = { start: lemq.initial }
# In the first loop, "finally" is filled with states from lemq and
# new_t that need to be reconnected:
finally = []
todo = [(start,start)]
while todo:
src,lemq_last = todo.pop()
for left, right, trg in transitions[src]:
if not isTag(left):
lemq.linkStates(src, trg, label)
if trg,trg not in seen:
todo.push((trg, trg))
else:
if src == lemq_last
new_t.linkState(start, trg, epsilon)
else:
new_t.linkState(src, trg, label)
if src in finals:
finally.insert((src, lemq_last))
if src,lemq_last not in seen:
todo.push((trg, lemq_last))
seen.insert((src, lemq_last))
# lemq_last was the last non-tag connected to the tag sequence that lead to lasttag:
for lasttag, lemq_last in finally:
newlemq = Transducer(lemq) # copy lemq
newlemq.finals = set(lemq_last) # let lemq_last be the only final state in newlemq
newlemq.minimize()
new_t.insertTransducer(lasttag, newlemq) # append newlemq after finaltag
return new_t
+ type multiwords
join (<j>) is handled by setting the next trimmer (bidix) target state to be trimmer.initial, so we simply skip to the start.
+ and # together
However, if we have a + followed by a # in monodix, we need to get back to where we were after reading the + part. An example:
monodix, one entry: foo<n><ind>+bar<pr># fie bidix, two entries: foo# fie<n> bar<pr> preprocessed (prefixed+lemq-moved) bidix, two entries: foo<n>[<n>|<ind>|<pr>]*# fie bar<pr>[<n>|<ind>|<pr>]*
So we start by matching
foo<n><ind> + bar<pr> # fie g i j k foo<n>[<n>|<ind>|<pr>]* # fie l m
and get as far as state pair (i,m), having consumed
foo<n><ind>
before seeing a +.
Now, the next SearchState records both the next monodix state (j, the state after +), the next bidix state (l, the bidix initial state), and the bidix state we were in when we saw the plus (m, at the end of the bidix tag list). So in the code SearchState next = (this_trg, trimmer.initial, trimmer_src).
Now we've consumed
foo<n><ind>
and have
bar<pr># fie
left, and can read from bidix initial. We match all of
bar<pr>
and then see a #. Since the third part of SearchState is set to some state S and we've seen a #, we jump back to that state S, from where we can match # fie, and we're done.
Compounds vs trimming in HFST
The sme.lexc can't be trimmed using the simple HFST trick, due to compounds.
Say you have cake n sg, cake n pl, beer n pl and beer n sg in monodix, while bidix has beer n and wine n. The HFST method without compounding is to intersect (cake|beer) n (sg|pl) with (beer|wine) n .* to get beer n (sg|pl).
But HFST represents compounding as a transition from the end of the singular noun to the beginning of the (noun) transducer, so a compounding HFST actually looks like
- ((cake|beer) n sg)*(cake|beer) n (sg|pl)
The intersection of this with
- (beer|wine) n .*
is
- (beer n sg)*(cake|beer) n (sg|pl) | beer n pl
when it should have been
- (beer n sg)*(beer n (sg|pl)
Lttoolbox doesn't represent compounding by extra circular transitions, but instead by a special restart symbol interpreted while analysing.
lt-trim is able to understand compounds by simply skipping the compund tags